Bell Test as a "Double-Slit for Two"

One of the physics' most misunderstood experiments

Forget everything you've heard about quantum "spookiness," instant communication across the entire cosmos, or consciousness creating reality from two different realities (wave vs. quantum). The Bell test—physics' most misunderstood experiment—actually reveals something more precise and beautiful: nature is composed of waves of possibilities, not just the predetermined lists of outcomes. Think of it as a double-slit experiment for two particles. Just as single-particle interference proves waves exist, Bell correlations prove those waves persist even across separated detectors. No magic, no paradox—just waves combining in ways classical physics can't reproduce. The math is straightforward: classical correlations max out at 2, while quantum reaches 2√2, which is precisely the theoretical limit for any information transfer. That's it. Here's the real story, without the myths.

Marek Španěl

Člověk

26. srpna v 12:57

Introduction: Why Is This Fascinating?

The Bell test is arguably one of the most profound experiments in modern physics, demonstrating that nature operates differently from classical intuition. Myths persist—instant communication, telepathy, mind over matter—but the real lesson is subtler: nature adds amplitudes (waves of possibilities), not just probabilities.

A paper by John Bell published on 4 November 1964 laid the foundations for the modern field of quantum-information science

Core Principle

Classically, we add probabilities. Quantum mechanically, we add amplitudes and only then square to get probabilities. The Bell test asks which rule nature follows when two distant, space-like separated measurements are made.

*Note: formulas use radians; angles in text are in degrees for readability.*

Double-Slit: Single-Particle Interference

In a double-slit, amplitudes from the two paths add and are then squared, producing fringes:

?math-blockP(x) \propto \cos^2\phi(x)?math-block

(up to the single-slit envelope). If you mark "which-path" information (e.g., with a slit detector or path-tagging polarisers), single-detector interference disappears: you're effectively adding probabilities. A quantum eraser can restore interference in appropriately post-selected data once the path information is erased—illustrating the rule: let waves combine, and a pattern emerges.

Quantum Eraser: No Changing the Past

Take an entangled pair. The signal passes through a double-slit; its paths are tagged, so singles show no fringes. Measure the idler in the diagonal basis ?math-inline|\pm\rangle = (|H\rangle \pm |V\rangle)/\sqrt{2}?math-inline : in coincidences, "signal | idler=?math-inline+?math-inline " yields fringes ?math-inline\propto \cos^2\phi(x)?math-inline and "signal | idler=?math-inline-?math-inline " yields complementary fringes ?math-inline\propto \sin^2\phi(x)?math-inline (shifted by half a period). Summed together, they cancel, hence no fringes in singles.

Quantum eraser pattern — Quantum eraser with 𝜙 ∈ [ − 𝜋 , 𝜋 ] ϕ∈[−π,π]: coincidence fringes cos ⁡ 2 𝜙 cos 2 ϕ and sin ⁡ 2 𝜙 sin 2 ϕ and their singles sum (flat, dashed).

Key point: nothing retrocausal happens—the signal hit its detector long before. You're just sorting existing data by the idler's outcome. It's like having two mixed jigsaw puzzles, and only by the colour of the back side can you tell which pieces belong together. The pattern lives in the correlations.

Bell: The Same, but in Correlations Between Two Detectors

For a maximally entangled photon pair, each wing is locally unbiased:

?math-blockP(A = +1 \mid a, b) = P(A = +1 \mid a) = \frac{1}{2}.?math-block

Fringes don't appear locally; they appear in coincidences. Define the correlation (with ?math-inlineA, B \in \{\pm1\}?math-inline ):

?math-blockE(a,b) = \langle AB \rangle = \frac{N_{++} + N_{--} - N_{+-} - N_{-+}}{N_{++} + N_{--} + N_{+-} + N_{-+}}.?math-block

For linear-polarisation singlet/triplet states one finds (sign depends on state/labelling)

?math-blockE(\Delta) = \pm\cos(2\Delta), \quad \Delta = a - b.?math-block

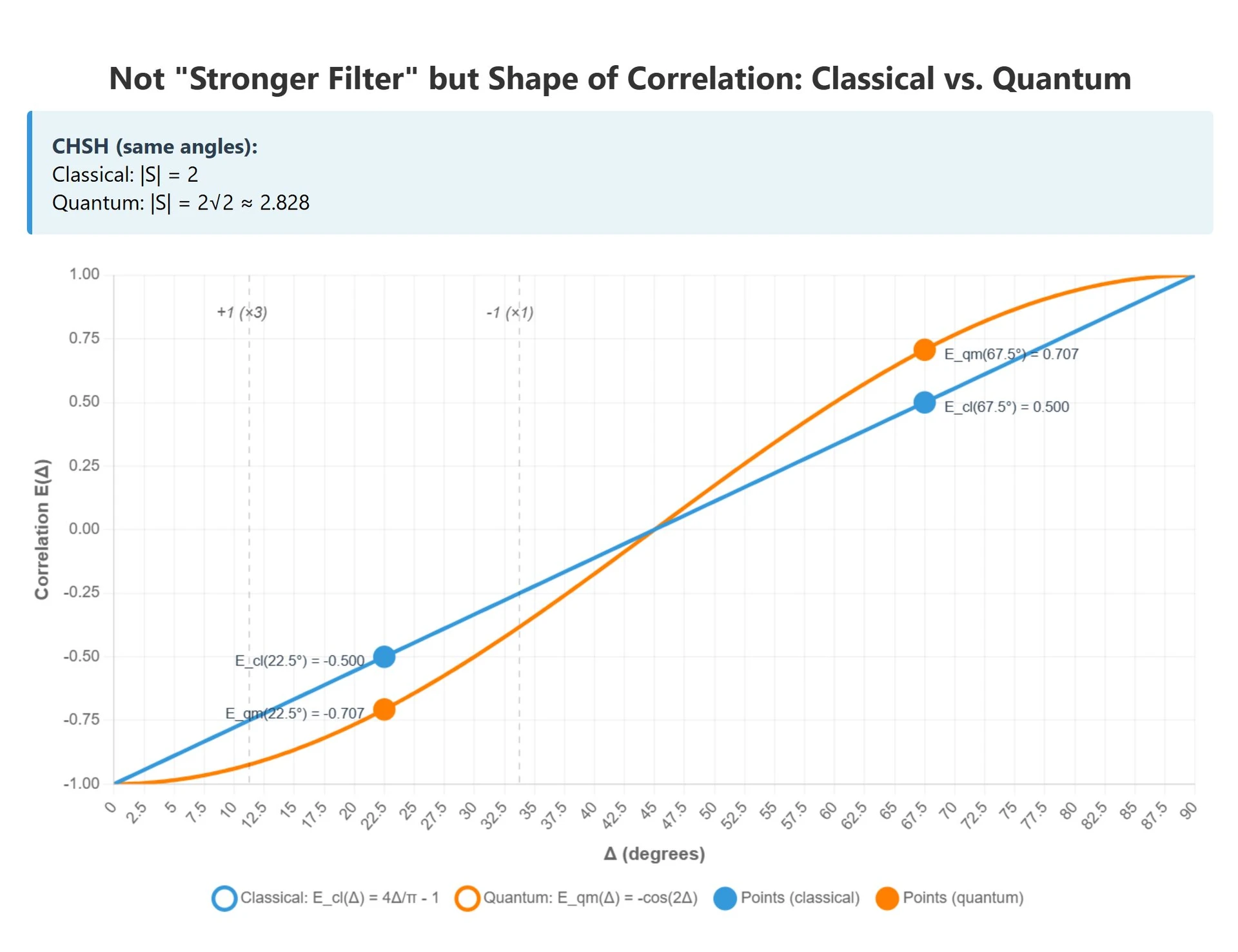
This is the "interference curve" in correlation space. Local realism (predetermined values) yields a piecewise-linear triangular dependence,

?math-blockE_{\text{LHV}}(\Delta) = 1 - \frac{4|\Delta|}{\pi} \quad \text{for } 0 \leq \Delta \leq \frac{\pi}{2}, \text{ period } \pi,?math-block

not a cosine. The difference is the shape vs. ?math-inline\Delta?math-inline : cosine vs. triangle.

Why We Get ?math-inline2\sqrt{2}?math-inline and Not Just 2

The CHSH parameter combines four correlations:

?math-blockS = E(a,b) + E(a,b') + E(a',b) - E(a',b').?math-block

With an optimal choice (e.g., ?math-inlinea = 0°?math-inline , ?math-inlinea' = 45°?math-inline , ?math-inlineb = 22.5°?math-inline , ?math-inlineb' = -22.5°?math-inline ) this reduces to

?math-blockS = 3E(\Delta_1) - E(3\Delta_1), \quad \Delta_1 = 22.5° = \pi/8.?math-block

* Local realism (triangle): ?math-inlineS \leq 2?math-inline (and equals 2 at ?math-inline\Delta_1 = \pi/8?math-inline ). * Quantum (cosine): ?math-inlineS = 3\cos(\pi/4) - \cos(3\pi/4) = 2\sqrt{2}?math-inline (Tsirelson bound).

It's pure geometry: the curved cosine lets the sum exceed the piecewise-linear envelope.

What Are "Incompatible" Measurements and Why Are They Needed?

Each side must have two settings that cannot be measured simultaneously on the same photon (non-commuting observables). If one global "preassigned-answers table" existed for all four settings, then necessarily ?math-inline|S| \leq 2?math-inline . Quantum theory forbids such a table, so ?math-inlineS?math-inline can exceed 2.

Why This Isn't "Spooky Action at a Distance"

For any choices ?math-inlinea, b?math-inline , each local outcome distribution is 50/50. No message can be sent; only joint correlations change. With space-like separation of choices/outcomes, relativity is safe. As in the eraser: the pattern appears only in coincidences.

Microscopic View: "Double-Slit Distributed Between Two Detectors"

For ?math-inline|\Phi^+\rangle = \frac{1}{\sqrt{2}}(|HH\rangle + |VV\rangle)?math-inline , the "++" amplitude at angles ?math-inlinea, b?math-inline is

?math-block\mathcal{A}_{++} = \frac{1}{\sqrt{2}}(\cos a \cos b + \sin a \sin b) = \frac{1}{\sqrt{2}}\cos(a - b).?math-block

Thus ?math-inlineP_{++} = \frac{1}{2}\cos^2(a - b)?math-inline , and similarly for "--". The two coherent "paths" (HH and VV) interfere, giving ?math-inline\cos(2\Delta)?math-inline in ?math-inlineE(\Delta)?math-inline . The interference shows up not as spatial fringes but as a correlation pattern.

Broader Context

Quantum theory is not the "most nonlocal" conceivable no-signalling theory. Hypothetical no-signalling correlations (so-called PR boxes) would reach ?math-inlineS = 4?math-inline in CHSH. A PR box is a black box with inputs ?math-inlinex, y \in \{0,1\}?math-inline and outputs ?math-inlineA, B \in \{0,1\}?math-inline that always satisfies ?math-inlineA \oplus B = xy?math-inline : three input pairs yield equal outputs, one produces different outputs. Each wing is 50/50 (no signalling), but the correlations are stronger than those of quantum mechanics. Nature never realises these as it would in fact be against laws of entropy; it stops at Tsirelson's bound ?math-inline2\sqrt{2}?math-inline , suggesting quantum rules are finely balanced: no signalling, yet not "maximally nonlocal."

Why This Isn't a Paradox, but the Maximum Allowed

Bell correlations are not a paradox. They are the maximum consistent with forbidding "free information." Information causality states: if Alice sends Bob ?math-inlinem?math-inline classical bits, Bob cannot extract **more than ?math-inlinem?math-inline bits** of randomly accessible information—even with pre-shared resources.

Quantum mechanics respects this and therefore has the sharp bound ?math-inlineS \leq 2\sqrt{2}?math-inline (Tsirelson). Hypothetical super-quantum correlations (PR boxes) would give while still no-signalling and would let one extract more than one bit from a single bit, not observed in nature.

Modern, non-concatenated formulations of information causality derive Tsirelson's bound directly from ?math-inline\sum I \leq C?math-inline for a noisy classical channel: a compact, device-independent reason why nature never exceeds ?math-inline2\sqrt{2}?math-inline .

Bottom line: nature is just nonlocal enough—quantum-level correlations, but never a violation of information causality.

Physics Without Beginning or End: The Logical Spiral to Infinity - Blogosvět.cz

Cheat Sheet: What to Remember

Main idea: Bell test is a "double-slit for two." Entanglement + incompatible measurements give a cosine correlation that reaches ?math-inline2\sqrt{2}?math-inline an optimal angle; any classical preassigned-answers model stays at ?math-inline2?math-inline . Just like with the double-slit "eraser": when you let waves coherently combine, the pattern emerges— just in the Bell test, not on a screen, but in the numbers ?math-inlineE(\Delta)?math-inline .

Key numbers: - Classical limit: ?math-inlineS \leq 2?math-inline - Quantum (Tsirelson) bound: ?math-inlineS \leq 2\sqrt{2} \approx 2.83?math-inline - Information-causality limit: ?math-inlineS \leq 2\sqrt{2}?math-inline - Each detector alone: always 50/50

Essence: Interference manifests in correlations, not in local singles. No communication, no magic—just coherent addition of amplitudes.